How Retail Investors Can Apply the Holy Grail Principle

Introduction

In the world of investing, few ideas are as powerful—and as misunderstood—as diversification. Most investors have heard the advice “don’t put all your eggs in one basket.” But what does that really mean in mathematical and practical terms?

Behind this simple idea lies a deep and elegant truth that hedge funds like Bridgewater Associates, founded by Ray Dalio, have built entire empires upon. Dalio calls it his “Holy Grail of Investing”—a principle that mathematically shows how combining multiple uncorrelated return streams can reduce risk dramatically without necessarily lowering returns.

In this article, we’ll break down the mathematical intuition behind diversification, understand how correlation affects portfolio risk, and see how professional investors use this concept to construct robust portfolios.

Understanding the Core Concept: Diversification and Correlation

At its heart, diversification is about risk management—not simply owning more assets, but owning the right mix of assets.

Let’s start with a simple example. Imagine you have a few investments, each expected to return around 10% annually, with a risk (volatility) of 10%. If all of them move up and down together (that is, they are highly correlated), then your total risk doesn’t really change much, no matter how many you own.

However, if your investments move independently—or better yet, move in opposite directions when one goes down—you start to see the magic of diversification.

The key factor that determines this is something called correlation (ρ).

Correlation measures how similarly two assets move.
A correlation of +1 means they move perfectly together.
A correlation of 0 means their movements are unrelated.
A correlation of –1 means they move exactly opposite to each other.

Lower correlation means higher diversification benefits

The Mathematical Relationship

Let’s look at the simplified formula that shows how portfolio risk declines as you add more assets:

σp=σ×1N+ρ(1−1N)\sigma_p = \sigma \times \sqrt{\frac{1}{N} + \rho \left(1 – \frac{1}{N}\right)}σp=σ×N1+ρ(1−N1)

Where:

σp\sigma_pσp = portfolio’s total risk
σ\sigmaσ = risk (volatility) of each asset
NNN = number of assets
ρ\rhoρ = average correlation between assets

This equation shows two things very clearly:

As you add more assets (increase N), the portfolio risk declines.
As correlation (ρ) decreases, diversification benefits increase significantly.

If the assets are completely uncorrelated (ρ = 0), total risk declines much faster than if they’re highly correlated (ρ = 0.6).

Let’s explore this in practical terms

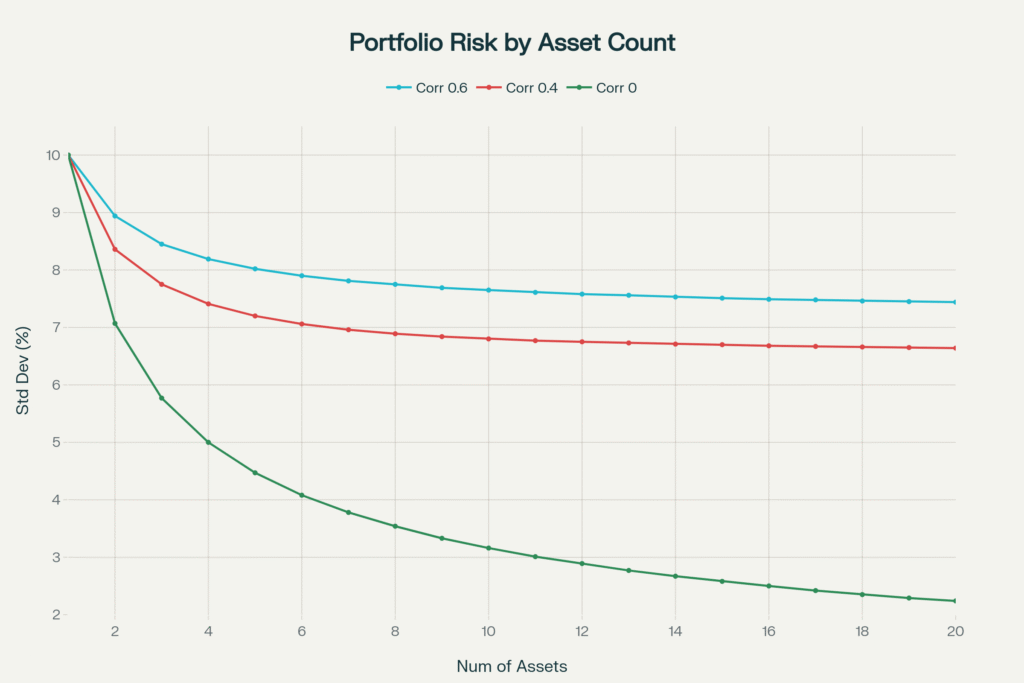
Impact of Asset Correlation on Portfolio Risk Reduction (10% Individual Asset Risk)

How to Interpret This Chart

The red line (correlation 0.6) shows very little reduction in risk with added assets; even with 20, diversification benefits are limited.
The blue line (correlation 0.4) offers moderate risk reduction as uncorrelated assets are added.
The green line (correlation 0) demonstrates the most powerful risk reduction—portfolio standard deviation falls sharply as you diversify, cutting risk by more than half at 20 uncorrelated assets.

Practical Scenarios: How Correlation Shapes Portfolio Risk

High Correlation (ρ = 0.6)

This is what happens when all your investments belong to the same theme—say, large-cap tech stocks or mid-cap Indian banks. Even if you own 20 of them, they’ll likely rise and fall together.

The diversification benefit is small.
Total portfolio risk might decline from 10% to only about 8.5–9%.
Beyond 4 or 5 assets, adding more doesn’t meaningfully reduce volatility.

This is why many investors feel diversified but aren’t. If all holdings react to the same macro factors (interest rates, oil prices, or global sentiment), true diversification is missing.

Moderate Correlation (ρ = 0.4)

Here, your portfolio starts including assets that behave differently—perhaps some equities, some bonds, and maybe a bit of gold or REITs.

The risk reduction becomes more visible.
Portfolio volatility may drop to 7–8% with around 10–12 assets.
However, after 15–20 assets, the benefit starts to plateau.

This is closer to a well-balanced multi-asset portfolio. It’s what many institutional investors aim for when managing retirement or sovereign wealth funds.

Low or Zero Correlation (ρ = 0 or close to 0)

This is where the magic happens. When return streams are uncorrelated, diversification becomes extremely powerful.

According to Ray Dalio’s findings, combining 15–20 uncorrelated return streams can reduce total portfolio risk by nearly 80%, while keeping expected returns the same.

In numerical terms:

If each investment has a 10% risk individually,
The portfolio’s total risk can drop to around 5% or even lower.

That means you’re achieving the same expected return but at half the volatility.

This significantly boosts your Sharpe ratio (return-to-risk ratio), allowing for higher compounded growth and a lower probability of loss.

Why the “Holy Grail” Works

Ray Dalio visualized this principle decades ago when building Bridgewater’s “All Weather” portfolio. He found that the marginal benefit of diversification declines as you add more assets—but up to a point, it’s extremely powerful.

With 1 asset, your risk is 100%.
With 2 uncorrelated assets, risk drops to ~70%.
With 5 uncorrelated assets, risk falls below 50%.
With 15–20, it stabilizes around 20–25% of the original risk.

Beyond that, adding more assets yields minimal improvement.

So the sweet spot often lies in combining 15–20 well-chosen, low-correlation return streams.

These can be different:

Asset classes (stocks, bonds, commodities, real estate)
Geographies (India, US, Japan, emerging markets)
Strategies (momentum, value, carry, mean-reversion)

This approach forms the core of modern portfolio theory (MPT) and the philosophy behind risk parity portfolios used by hedge funds.

From Theory to Practice: What It Means for Individual Investors

From Theory to Practice: What It Means for Individual Investors

You don’t need to be a hedge fund to apply this concept. Even retail investors can use diversification mathematically.

Here’s how you can put it into practice:

Mix Uncorrelated Assets – Don’t just buy multiple stocks. Combine equities, bonds, gold, and maybe international ETFs.
Study Correlations – Tools like Portfolio Visualizer or Morningstar can help estimate how your holdings move relative to each other.
Think in Terms of Risk Units – Instead of focusing only on expected returns, pay attention to how each asset contributes to total portfolio volatility.
Avoid Over-Diversification – After about 20 uncorrelated holdings, additional ones add little benefit and may dilute returns.
Rebalance Regularly – Market movements can change correlations over time. Rebalancing helps maintain your optimal mix.

The Real Edge: Compounding Without Fear

The greatest advantage of diversification isn’t just about protecting downside—it’s about allowing you to stay invested.

When your portfolio fluctuates less, you’re less likely to panic-sell during downturns. Lower volatility translates to steadier compounding. Over time, this psychological and mathematical stability makes a huge difference in wealth accumulation.

Dalio once said, “He who lives by the crystal ball will eat shattered glass.” Predicting markets is impossible—but constructing a portfolio that can withstand all kinds of weather is achievable.

That’s the true Holy Grail of investing.

Final Thoughts

Mathematics and investing might seem worlds apart, but in truth, they’re deeply connected. The equation of diversification isn’t just a formula—it’s a framework for thinking probabilistically and managing uncertainty.

Whether you’re a hedge fund manager or an individual investor, understanding the relationship between correlation, risk, and reward helps you build portfolios that are both smarter and safer.

In the end, successful investing isn’t about finding the perfect bet—it’s about combining many imperfect ones in a way that the whole becomes stronger than the sum of its parts.